Les mathématiques derrière le pic de Hubbert
En 1956, dans son article « nuclear energy and the fossil fuels » dans lequel il prédisait le pic de production des Etats Unis, le géologue King Hubbert avait utilisé 80 pages d’équations différentielles pour arriver à sa conclusion !
Voici ici quelques détails du calcul qui permit à Hubbert de déterminer le pic de production des Etats-Unis. Cette méthode est finalement assez simple et ne prend en compte que des données géologiques et aucune donnée politique.
Pour déterminer le pic de Hubbert, on a besoin de deux types de données :
- La production annuelle de pétrole : P
- La production cumulée c'est-à-dire la somme des production annuelle depuis le début d’exploitation d’un champ ou d’une région pétrolifère : Q
On rappelle que les Etats-Unis ont passé leur pic en 1971. Les données P et Q sont en ligne sur le site de l’AIE et sur le site de l’ASPO.
On trace tout d’abord P/Q en fonction de Q
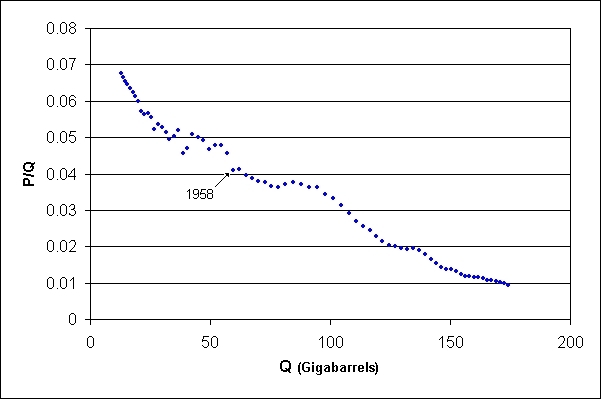
La première partie de la courbe n’est pas très régulière mais on remarque que la seconde partie de la courbe peut être approximée à une droite d’équation y = mx + a où m est la pente de la droite et a l’ordonnées à l’origine
On trouve aisément m et a.
On note aussi Q t la valeur de Q pour laquelle P/Q est nulle. C'est-à-dire l’intersection de notre droite avec l’axe des abscisses. Ceci se vérifie quand P = 0 c'est-à-dire quand la production est à l’arrêt. Q t est la valeur de la production cumulative maximale qui pourra être atteinte. C’est la quantité totale de pétrole extrait. Elle est de 198 Gb environ. De plus, il est facile de déterminer la date du pic car il a lieu quand on a produit la moitié de la quantité totale de pétrole qui pourra être prélevée c'est-à-dire quand Q = Q t/2. On la place en 1973 avec 99.198 Gb.
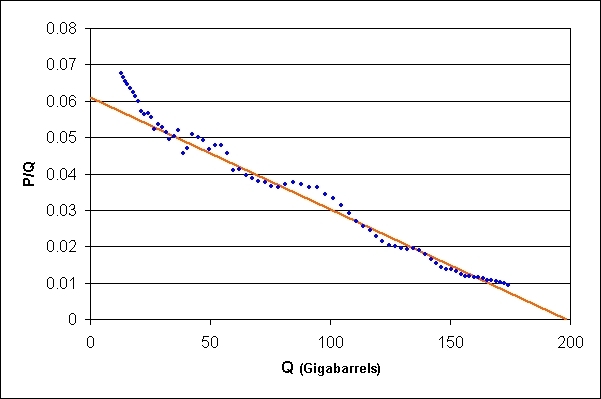
On voit donc que la théorie de Hubbert est donc de supposer linéaire la relation entre P/Q et Q…
Exprimons maintenant P en fonction des autres données du problème.
P/Q = mQ + a
P/Q = -aQ/Q t + a en appliquant la formule au point (Q t, 0), on trouve m
P/Q = a(1 - Q/Q t)
P = a(1 - Q/Q t)Q
a est facilement accessible c’est l’ordonnée à l’origine que l’on trouve graphiquement comme l’intersection de la droite avec l’axe des ordonnées.
La terme (1 - Q/Q t) est la fraction de pétrole encore exploitable. En effet, on peut lire cela de la manière suivante : (Q t-Q)/ Q t ; Quantité de pétrole que l’on peut encore récupérer sur quantité de pétrole récupérable totale.
On remarque que notre capacité à produire du pétrole à un moment donné est linéairement dépendante de la quantité de pétrole encore disponible pour l’exploitation.
Il est plus intéressant de discuter sur l’inverse de cette équation.
1/P = 1/[a(1 - Q/Qt)Q]
1/P s’exprime donc en années par gigabaril.
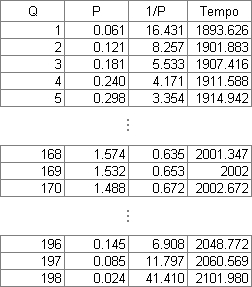
Sur une feuille de calculs, on peut maintenant pour chaque valeur de Q variant de 1 à Q t calculer P et 1/P et enfin le temps grâce à l’expression obtenue plus haut
Il nous faut aussi calculer la colonne temps. Il est facile d’y arriver en sachant que fin 2001 169 Gb ont été produits en tout (Q production cumulée). C’est sur cette unique donnée que nous nous appuyons. Pour les autres cases de la colonne temps, il suffit d’ajouter ou de soustraire les valeurs de 1/P de la ligne qui correspond car Q varie d’un Gb à la fois et 1/P représente des années par Gb.
Enfin, il suffit de tracer le graphe P=f(t).
Et voilà votre courbe de Hubbert.

A l’échelle mondiale, on peut bien sûr appliquer une telle méthode. On se base sur les données disponibles dans le « BP Statistical Review » et sur celles de « l’ASPO »

On retrouve le même début chaotique et la droite de la deuxième partie de la courbe
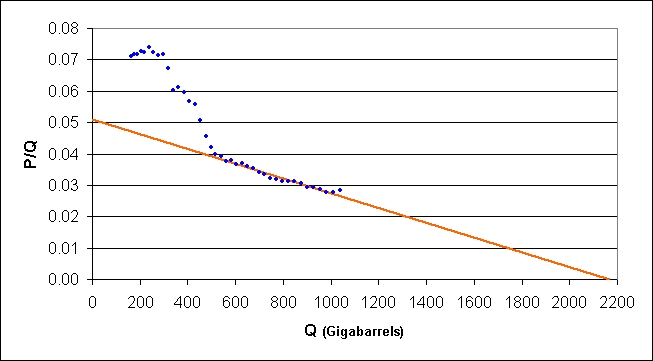
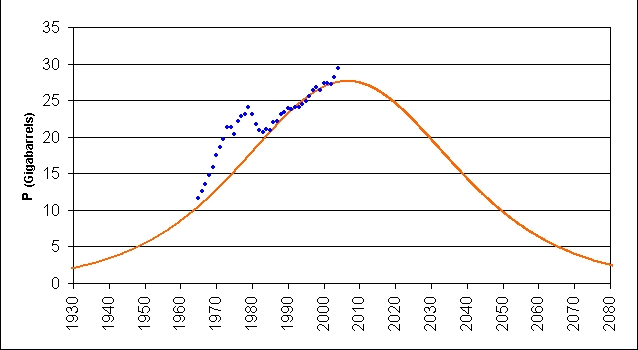
Et un pic prévu pour 2006 !
Conclusion :
Connaissant maintenant les méthodes de calculs qui se cachent derrière la courbe de Hubbert, nous pouvons analyser les raisons pour lesquels certaines dates des pics différents.
En fait, ces différences sont essentiellement liées aux données. Différentes types de données donnent bien évidemment des résultats différents.
|