COMMENT COMPRENDRE LES CONCEPTS FONDAMENTAUX DE LA MODELISATION EN QUELQUES QUESTIONS ET UN EXEMPLE
Cet article a été réalisé grâce aux documents fournis pour nos recherches par Guillaume Chapron, Laboratoire d’écologie, CNRS UMR 7625, Ecole Normale Supérieure, 46 rue d’Ulm, 75230 Paris cedex 05, France.
Pourquoi modéliser des populations ?
- Pour comprendre l’écologie des populations
- Pour étudier la dynamique des populations
- Pour élaborer et proposer de nouvelles stratégies de contrôle des populations
Pourquoi modéliser les populations pour contrôler ?
- Est-ce qu’une population va s’éteindre si on la prélève de 10% par an
- Est-ce que la taille de la population actuelle est viable ? (va-t-elle s’éteindre ?)
- Comment contrôler l’expansion d’une population ?
Qu’est-ce qu’une modélisation de populations ?
- On attend par modélisation formalisation mathématique d’un processus démographique
- La modélisation de population est largement employée dans le suivi et le contrôle des populations. Elle est plus connue sous le terme de Population Viability Analysis ou PVA.
Quels modèles pour quelles populations ?
- Il faut avant tout choisir l’échelle à laquelle on se place. Cette échelle est choisie en fonction des résultats que l’on souhaite et des données à la notre disposition
- Il faut commencer par des modèles simples qui se concentrent sur les facteurs clés
- Ensuite seulement la complexité du modèle est augmentée
Comment construit-on un modèle démographique ?
- Il faut connaître la biologie de l’espèce étudiée
- Il faut ensuite sélectionner les caractéristiques des individus qui nous intéressent dans la population
- La construction du modèle ensuite se déroule en trois étapes :
- Détermination des différentes classes dans la population

- Détermination des mécanismes de transition entre les classes
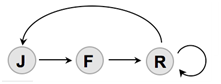
- Expression des lois de transitions
Il faut la probabilité qu’une transition ait lieu en fonction de la taille de la population.
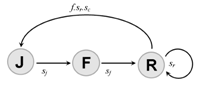
Il faut la probabilité qu’une transition ait lieu en fonction de la taille de la population.
- A partir de ce cycle de vie, on peut bâtir des modèles dont la complexité est croissante : déterministe, stochastique voire des modèles prenant en compte l’individu lui-même, des variations d’environnement, des variations génétiques…
Les avantages du modèle déterministe
- Il ne demande que peu de données et est très pertinent
- Il bénéficie de toute l’algèbre liée aux matrices
- Il permet de prévoir des résultats très importants comme de taux de croissance d’une population
La matrice de transition
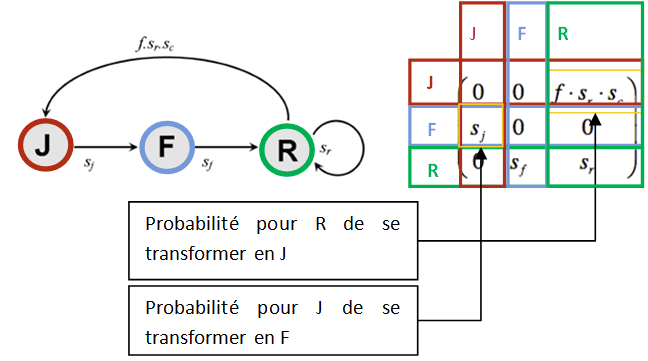
On peut ainsi facilement accéder à la population présente à t+1 connaissant celle à t :
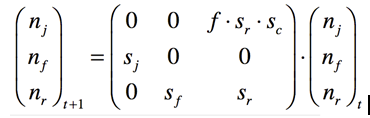 Les matrices sont très faciles à implémenter ce qui facilite la traduction informatique du modèle.
Les matrices sont très faciles à implémenter ce qui facilite la traduction informatique du modèle.
Les informations principales obtenues à partir de la matrice de transition
- Le taux de croissance d’une population : ?
- ?>1 : augmentation de la population
- ?=1 : stabilisation de la population
- ?<1 : diminution de la population
- L’importance relative des différentes classes
- La contribution de certaines classes à la reproduction
- La sensibilité du taux de croissance suivant les paramètres
Qu’est-ce que la stochasticité ?
- Stochasticité vient du grec stokhastês qui signifie « prédit l’avenir » et « parvient à son but »
- En modélisation « stochastique » est utilisé pour définir des processus dont l’évolution s’étudie au moyen de probabilités
Deux types d’extinction ?
- Déterministe : l’évolution de la population est connue avec certitude : elle est condamnée à disparaître
- Stochastique : l’évolution n’est pas connue parfaitement : la population peut disparaître ou pas
- Pourquoi les espèces disparaissent-elles ?

Effet allee : lorsque que la densité de population est faible, la fertilité étant liée à la densité de population devient très faible et peut entraîner une extinction de l’espèce
- Trois types de stochasticité ?
- Démographique :
-
- Hasard lié à la survie et aux naissances
- Changements de taille de population, des différentes classes et du ratio des mâles et des femelles
- Environnementale
- Entraine des changements dans le taux de fécondité et de survie
- Hivers rudes, sécheresses, maladies…
- Quand les variations sont trop importantes, cela devient des catastrophes
- Génétique
- Hasard intrinsèque de la méiose et de la fécondation
- La perte d’allèles rares suite à un autre effet
- Une perte d’hétérozygotie par le brassage génétique
- La fixation d’allèles détériorés par la consanguinité
- Les populations de petite taille sont nettement plus sensibles au hasard que les autres.
Les modèles déterministes et les modèles stochastiques ?
- Avec un modèle déterministe, on obtient le taux de croissance d’une population, le temps nécessaire pour obtenir une structure stable, des valeurs reproductibles, la sensibilité des variables aux paramètres
- Avec un modèle stochastique, on obtient la probabilité d’extinction
Comment implémenter un modèle stochastique ?
- Construisons un modèle stochastique simple
- Le taux de survie suit une loi binomiale (par exemple)
- Le taux de fécondité suit une loi de Poisson (par exemple)
- On lance de multiples trajectoires de populations en changeant la taille initiale de la population et on regarde quelles populations disparaissent
- On obtient par exemple le résultat suivant en effectuant une simulation de Monte-Carlo en modifiant la taille de la population initiale :
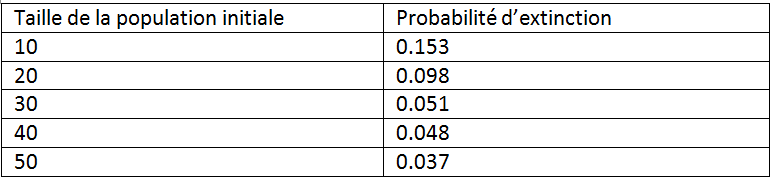
On choisit un taux acceptable de risque d’extinction.
On peut alors trouver une taille minimale nécessaire pour que la population soit viable.
C’est un modèle régit par le système de deux équations suivantes :
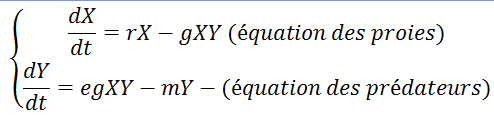
- r : taux de croissance de la population des proies
- g : taux d’efficacité de la prédation des individus Y sur X
- e : coefficient de conversion : nombre de jeunes prédateurs générés par proie capturée
- m : taux de mortalité des prédateurs
Attention :
- s’il n’y a plus de prédateurs, le modèle prévoie une croissance exponentielle des proies alors qu’elle est aussi régulée par les ressources.
- g dépend du nombre de proies : g(X)
On a ainsi un nouveau système d’équations :
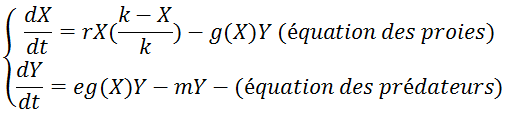
On peut déterminer g(X) en divisant la journée en différentes phases :
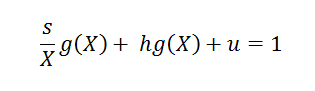
- s/X correspond au temps de recherche des proies
- h est le temps moyen nécessaire pour attraper une proie
- u correspond aux autres occupations
En posant :
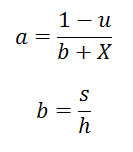
On a :
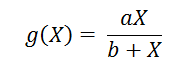
D’où :
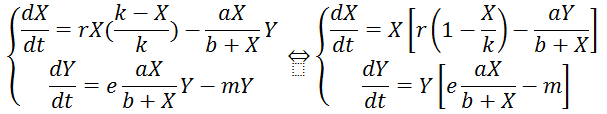
Le degré de mimétisme des proies est non constant dans le temps : selon la saison, les proies sont plus ou moins faciles à rechercher. Donc s varie avec une période de l’année.
On peut donc réaliser le modèle avec r, k, a, e, m constants et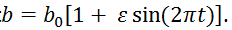
Pour e=0, on a déjà un comportement complexe du système :
- bifurcation supercritique de Hopf pour la valeur
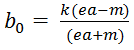 : c’est une évolution critique cyclique de période
: c’est une évolution critique cyclique de période 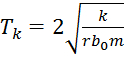
- Bifurcation transcritique pour
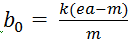 . Si b0 est strictement supérieur à ce rapport, alors on a extinction des prédateurs quelles que soient X0 et Y0
. Si b0 est strictement supérieur à ce rapport, alors on a extinction des prédateurs quelles que soient X0 et Y0
- Entre ces 2 valeurs, on a une évolution vers un état stationnaire
Revenir en Haut de Page






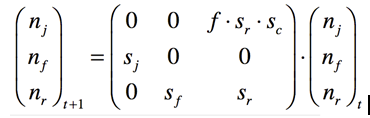


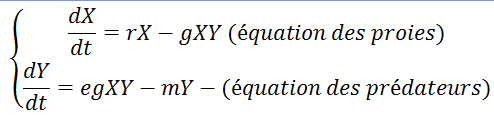
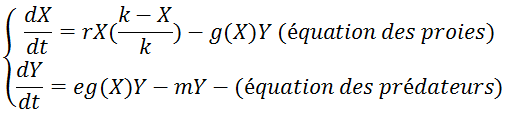
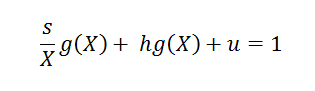
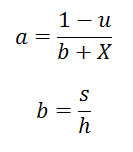
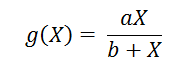
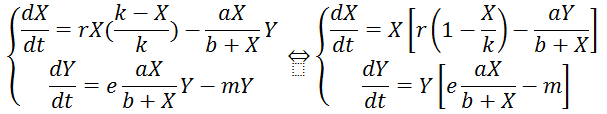
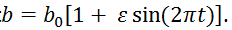
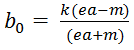 : c’est une évolution critique cyclique de période
: c’est une évolution critique cyclique de période 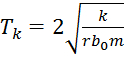
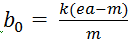 . Si b0 est strictement supérieur à ce rapport, alors on a extinction des prédateurs quelles que soient X0 et Y0
. Si b0 est strictement supérieur à ce rapport, alors on a extinction des prédateurs quelles que soient X0 et Y0