Ce modèle est un modèle mathématique de marché qui évalue la valeur d’une action selon un processus stochastique. Sa grande particularité est de mettre en relation le prix implicite de l’option considérée avec les variations de prix de l’actif étudié. En 1997, Scholes et Merton reçoivent le prix Nobel de l’économie pour leurs travaux.
Ce modèle est fondé sur certaines hypothèses qui sont nécessaires à la démonstration de la formule. Hypothèses du modèle de Black & Scholes :
-Le prix de l’actif suit un mouvement brownien, la volatilité et la dérivée de ce prix sont considérées constantes
-Il n’y a pas d’opportunité d’arbitrage
-Le temps est une fonction continue
-Les ventes à découvert sont autorisées
-Les coûts de transactions sont supposés nuls
-Le taux d’intérêt sans risque connu à l’avance et constant
-Aucun dividende n’est versé entre le moment où l’action est évaluée et l’échéance

Ces hypothèses sont au fondement de l’élaboration de la formule de Black & Scholes, mais il s’avère qu’elles ne sont pas toujours valables sur les marchés financiers, remettant ainsi en question la pertinence du modèle utilisé. Ainsi le temps n’est pas toujours continu en finance, et la formule n’est donc plus vérifiée lorsque la fréquence des discontinuités de cours augmente trop, ce qui est notamment le cas en temps de crise. Ainsi, utiliser Black & Scholes en période de crise ne fait qu’aggraver la situation, au sens où la formule est utilisée dans un contexte où elle n’est plus valable. Par ailleurs, l’évaluation de la volatilité qui est une constante n’est pas si évidente que ça et amène à des difficultés. Comme celle-ci n’est en fait pas tout à fait une constante, puisqu’elle dépend du prix d’exercice et de la maturité, l’écart entre le modèle et la réalité est bien effectif.

Le modèle a d’ailleurs subi des modifications afin de pallier les imperfections que nous avons énoncées précédemment. Ci-dessous, un exemple de modification du modèle afin de pricer les options européennes payant des dividendes, formule plus connue sous le nom de Black-Scholes-Merton. Pour les options sur les indices, tels que le CAC 40, où pour y figurer les entreprises doivent payer des dividendes, on peut supposer que les dividendes sont versés de façon continue.

On note alors ce paiement sur une période dt :
q St dt : avec comme paramètre un q constant

Sous cette formulation le prix arbitrage-libre selon le modèle Black-Scholes peut être montré comme étant :

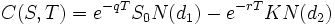
Espérance sous probabilité risque neutre du pay off terminal

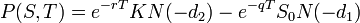
prix théorique d’une option de vente, de pay-off

D’où maintenant :

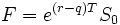
est le prix modifié en avance qui se produit aux termes d1 and d2.

Extrait de : Lien