
I. Récapitulatif historique de la formule de Black & Scholes
La formule de Black & Scholes est très largement fondée sur les travaux de Louis Bachelier, père des mathématiques financières modernes qui présente en 1900 sa thèse « Théorie de la spéculation, annales scientifiques de l’ENS ». Dans celle-ci, il développe sa théorie des probabilités et des processus aléatoires, ainsi que leurs applications. C’est seulement en 1973, soit près de trois quart de siècle après la théorie de Bachelier, que la formule de Black & Scholes est introduite sur le marché financier. Très vite, ils connaîtront un vrai engouement pour cette formule qui présente deux avantages : son objectif est attirant (optimiser la politique d’investissement grâce à un nouvel outil) et son utilisation est très simple. En 1997, la formule recevra le prix Nobel de l’économie mais c’est en cette même année que l’entreprise LTMC (Long Term Capital Management) fait faillite alors qu’elle était conseillée par Scholes et Merton. S’en suit la crise de 1998, où la confiance des financiers en cette formule est sérieusement remise en cause. Malgré tout, son utilisation continue encore jusqu’à nos jours, mais de façon plus modérée.
II. Parallèle avec le mouvement Brownien
Le précurseur des mathématiques modernes, Louis Bachelier, a inspiré Einstein sur ses travaux à propos du mouvement Brownien, datant de 1905, soit cinq ans après la parution de sa thèse « Théorie de la spéculation, annales scientifiques de l’ENS ». Cette interaction des deux disciplines, physique et mathématiques financières, ne cessera de se vérifier par la suite. Paradoxalement, il semble que ça soit les mathématiques financières qui à l’origine inspirèrent la physique moderne. Par ailleurs, les similitudes sont frappantes lorsqu’on réalise que chacune de ces disciplines prenne en compte l’interaction d’un grand nombre d’acteurs mais que les déterminismes individuels sont oubliés au profit de phénomènes collectifs. Ainsi il y aurait une micro et une macro économie au même titre que la physique microscopique et macroscopique. D’un point de vue théorique, la démarche afin d’obtenir un résultat chiffré est la même : on modélise le mouvement d’une particule brownienne en modélisant les chocs désordonnés qu’elle subit par une seule valeur, la température. A partir de celle-ci, supposée homogène et décrivant parfaitement le milieu dans lequel évolue la particule Brownienne, on suppose pouvoir modéliser le mouvement associé à la particule. Pour la valeur d’une action, on modélise ses fluctuations passées (ordre d’achats et de vente) et on en déduit de la même façon sa valeur actuelle. Ci-dessous, les courbes décrivant les évolutions du mouvement brownien et de valeur suivant la formule de Black & Scholes.
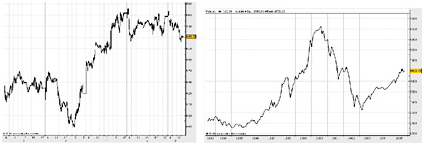
Variations de l’indice CAC 40 par minute (à gauche) et par mois (à droite)
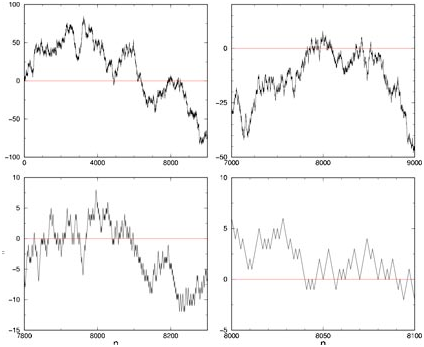
Marche aléatoire, modèle idéalisé, du mouvement brownien
On observe à l’œil nu, mais cette observation a été vérifiée par des analyses de Fourier, une ressemblance globale entre les deux courbes. En outre, toutes deux ont la propriété d’auto similarité, c’est-à-dire, qu’elles conservent cette allure quelque soit l’échelle des abscisses. Les hypothèses similaires des deux théories semblent donc amener à des résultats analytiques proches. C’est pour ces raisons que l’on peut parler de véritable parallèle entre la théorie du mouvement brownien et celle de la modélisation mathématiques financière. Malgré le succès e la théorie d’Einstein qui n’a pas encore été remise en cause, il semble que le modèle mathématique associé soit largement critiqué par une partie des acteurs financiers.
III. Données techniques sur l’approche de Bachelier
Il est intéressant de comprendre l’approche de Bachelier afin de véritablement mettre en avant les hypothèses qui sont à l’origine de ce modèle et qui ont été tout au long de la fin du XXème siècle remises en cause. L’article dont nous parlons met clairement en évidence l’élaboration de la formule à laquelle Bachelier aboutit, nous ne nous contenterons donc juste de le citer :
[Considérons un actif financier (une action, une obligation, un cours en Bourse, le prix de la tonne de sucre, etc.). Son prix S, qui fluctue de façon erratique, peut être considéré comme la somme de ses variations (à laquelle on ajoutera à la fin sa valeur initiale S0). Simplifions en supposant que :
— les variations ne peuvent prendre que les valeurs (+/- h) et ce avec la même probabilité,
— ces valeurs sont prises à des pas de temps réguliers tau,
— les variations sont des variables aléatoires indépendantes .
Nous discuterons plus loin l’importance et la validité de ces points. Écrivons que l’événement « le prix de l’actif vaut S à l’instant (t+tau) » résulte de deux événements disjoints de probabilité 1/2 : « il valait s – h ou s + h à l’instant antérieur t. On a, avec des notations évidentes :
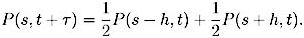
Soit en retranchant P(s,t) aux deux membres :
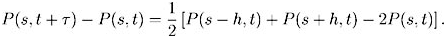
On suppose que P(s,t) est une fonction continue et qu’elle admet un développement de Taylor, en se limitant à l’ordre le plus bas en tau et h, il reste :
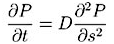 (1)
avec
(1)
avec
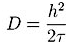 (2)
(2)
Si l’on suppose maintenant que les pas en temps et dans l’espace tendent vers 0, mais de sorte que D reste fini, on a affaire à une équation différentielle aux dérivées partielles. On vérifiera que l’équation suivante est une solution de cette équation :
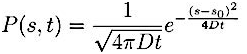
On donnera à l’exercice 2 (fiche élève, rubrique « En pratique ») une dérivation combinatoire directe de cette équation.
P(s,t) est devenue une densité continue de probabilité. Ce qui veut dire que la probabilité que le prix de l’action soit compris entre S et S+dS peut s’écrire :
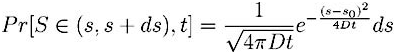
On remarque que Bachelier a ainsi retrouvé l’équation de la chaleur en (1) et qu’il a appelé D le coefficient d’instabilité. Nous parlons actuellement de volatilité du cours qu’on associe au risque. Il est clair que cette approche préfigure celle d’Einstein cinq ans plus tard.
IV. Limites du modèle
Le modèle de Bachelier est basé sur le simple fait que le prix d’un actif S est la somme de ses variations (augmentée de sa valeur initiale, qu’on prendra nulle pour alléger l’écriture). Soit : 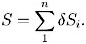
Et donc que sa loi de distribution est donnée par le théorème de la limite centrale (TLC). Soit : 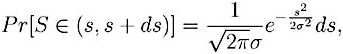
Avec sidma=n*sigma*dS où sigma*dS est la variance des accroissements dS.
Mais il y a deux limitations fortes à cette approche.
La première est que le théorème de la limite centrale est une loi asymptotique, d’autant mieux vérifiée que est grand, mais aussi que est petit. Il en ressort que les queues de distribution ne sont jamais bien reproduites (par exemple dans l’équation, peut varier sur tout même si la variable aléatoire dont elle est la somme est bornée).
La seconde est que le théorème de la limite centrale suppose des hypothèses contraignantes :
— les tirages des dS sont indépendants ;
— ils peuvent obéir à une loi de probabilité quelconque, pourvu que cette loi ait un fini et constant (loi étroite) ;
— le temps peut être considéré comme une variable continue.
Ces trois hypothèses sont mal ou pas vérifiées empiriquement.
Dans l’économie réelle, les variations de valeurs peuvent être fortement corrélées, l’effet « moutonnier » existe (cf. André Orléan, in Les Mathématiques sociales, « Pour aller plus loin »). Par ailleurs, les temps séparant les achats ou ventes peuvent être très brefs (de l’ordre de la seconde peut-être avec l’internet), ils ne sont pas infiniment petits. On a là un problème général souvent sous-estimé : dans les processus dynamiques, le passage en temps continu n’est pas anodin ; il peut même faire disparaître des solutions divergentes.
Le modèle de Black et Scholes est universellement répandu. C’est une stratégie de portefeuille fondée sur une formule qui est une sophistication du modèle de Bachelier. Par exemple, on considère plutôt la variation relative des actions dS/S = dlog S donc les distributions des actifs deviennent lognormales :
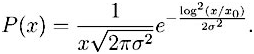
Il suffit de changer, dans la gaussienne, x en log(x) et donc aussi dx en dx/x . Il en conserve néanmoins les trois présupposés mal ou pas confirmés expérimentalement.
Tout cela fait que les queues de distribution prévues par ce genre d’approche sont mauvaises : les événements « anormaux » mais économiquement significatifs sont infiniment trop rares.
Bien des amendements ont été depuis portés au modèle de Black et Scholes pour rendre compte des données empiriques. Par exemple, on introduit une « volatilité effective » dépendante du temps qui est une nouvelle variable aléatoire ; c’est elle qui concentre pas mal d’informations manquantes.
Sources :
Controverse Mathématiques & Finance. Haut de page.
GILLET, LETOURNEAU, MAGNIEN, MARCILHACY, VYARAVANH-GIRARD