
Selon certains, David Li, et plus particulièrement sa formule sur les copules gaussiennes, serait responsable de la crise financière de 2008. Dans Wired Magazine, Félix Salmon en fait même dans un article de Février 2009 une "recette pour le désastre". David Li fait en effet parti des praticiens de la finance quantitative, essayant de calculer les risques financiers afin de les éliminer à coups de formules mathématiques. David X. Li est né dans les années 1960' en Chine sous le nom de Xiang Lin Li. Détendeur d'un master en économie de la Tianjin's Nankai University, d'un MBA de la Laval University au Québec et d'un PhD en statistiques de University of Waterloo en Ontario, il commence sa carrière à la CIBC (Canadian Imperial Bank of Commerce) et intègre l'unité de mesure des risques du groupe J.P. Morgan en 2000. C'est à ce moment qu'il publie son papier, au cœur du problème, «On Default Correlation: A copula function approach.», censé répondre au vieux problème de modélisation du comportement de plusieurs risques corrélés entre eux. Il y fournit en effet une formule, basée sur la fonction copule gaussienne, permettant de connaître la probabilité commune de défauts de paiements entre des produits constituants un CDO (Collateralized Debt Obligation, ensemble de produits vendus par paquet dont on peut acheter un certain pourcentage, et donc prendre plus ou moins de risques). Très utilisée dès l'instant de sa parution, cette formule est cependant totalement remise en cause depuis la crise car considérée comme responsable de la crise. A-t-elle alors une réelle implication ou constitue-t-elle seulement le bouc émissaire idéal?
I. Élaboration, utilisation et défaillances du modèle
L'élaboration de la formule répond à une demande simple mais a une réponse très complexe: l'évaluation de plusieurs risques de défauts de paiement corrélés entre eux. Elle est indispensable particulièrement pour évaluer le prix d'un CDO, car les défauts de paiement des parts du paquet sont extrêmement corrélés. L'observation de la corrélation est simple, sa modélisation l'est beaucoup moins. Les marchés ne constituent pas en effet des laboratoires isolés. La faillite d'une compagnie par exemple peut largement conduire à un environnement favorable à celles d'autres compagnies. Autre exemple: la crise financière en Russie qui a provoqué la chute des bons du trésor russes en 1998 a entrainé celle des bons du trésors mexicains. Li s'est alors inspiré des travaux réalisés par les sociétés d'assurance vie: dans un couple, la mort du partenaire augmente significativement les chances de décès de l'autre partenaire (un homme veuf a six fois plus de chances de mourir qu'un homme ayant encore sa partenaire). Le raisonnement est ensuite statistique, à la manière de la physique, et permet de modéliser fidèlement le comportement d'un ensemble de personnes grâce à la chaine de Markov. Si l'on traite les individus comme des atomes, on peut leur appliquer les mêmes mathématiques... Li écrit alors dans The Wall Street Journal: «J'ai réalisé que le problème que je tentais de résoudre était exactement similaire à celui de ces personnes. Les défauts d'un prêt correspondent à la mort d'une compagnie.», ce qui permettait de modéliser mathématiquement l'effet de la faillite d'une compagnie sur les chances de faillites des autres. Il décida alors d'utiliser une courbe très standard, la copule gaussienne, afin de déterminer la corrélation entre différents portefeuilles d'investissements. Cette copule gaussienne n'était pas nouvelle, c'est son application à la finance, et plus particulièrement aux CDO, qui l'était. Le prix des CDO, notamment ceux auparavant trop difficiles à évaluer, peut alors être connu précisément. Plus précisément (voir formule à la fin de l'article), sa théorie introduit une variable aléatoire, le «temps de survie», qui permet de définir la corrélation comme un coefficient de corrélation entre les deux temps de survie des titres. C'est alors qu'il se sert de la copule gaussienne pour calculer, à partir des données historiques des marchés, la probabilité commune de défaut de deux titres.
Tout le monde s'est alors jeté sur cette formule: investisseurs, régulateurs, banques et agences de rating ont été captivés par son élégance et sa simplicité d'utilisation. Les marchés de CDO et de CDS (Collateralized Swap Obligations) se sont développés ensembles, s'alimentant l'un l'autre. Tout était basé sur le formule de Li, applicable n'importe où, pour n'importe quoi. Selon Darrel Duffie, professeur de finances à l'Université de Standford, «Le monde de corporation de CDO s'est fondé presque exclusivement sur ce modèle». Le 10 Août 2010, l'agence de rating Moody's incorpore la formule dans sa méthodologie de notation. Une semaine après, Standard and Poor's change aussi la sienne. Les pratiques traditionnelles sont jetées par la fenêtre, on préfère mesurer le risque de façon mathématique donc certaine... Les agences de notations attribue alors des triple-A à énormément de paquet. Le marché des CDO et des CDS explose et atteint des niveaux inimaginables: celui des Swap passe de 920 milliards de dollars en 2001 à 62 trillions en 2007. Le modèle semble bien marcher dès lors que les marchés de l'immobilier et des bons du trésors continuent de croître. Mais l'explosion de la bulle du marché immobilier a eu un effet plus désastreux que prévu, à cause de la sous-évaluation des risques de corrélation. Au début, les banquiers n'étaient pas inquiets car la formule annonçait que les différents points du marché des États-Unis n'étaient pas corrélés. Cependant, les défauts de paiement continuaient d'augmenter alors que le modèle voyait le marché comme celui des années 1990', et pas comme l'excessif monstre d'inflation qu'il avait créé. Paradoxalement, c'est le modèle qui a changé la nature de la réalité qu'il modélisait, en influençant le comportement des acteurs. La panique sur le marché immobilier s'est alors répandu sur le marché des produits dérivés puis à toute l'économie. Soudainement, tout était profondément corrélé.
Comment se fait-il que la formule ait pu induire une si grossière erreur? Sur les marchés financiers, le mimétisme est une recette classique pour la création d'une bulle spéculative. Acheteurs et vendeurs de CDO peuvent être d'accord sur les prix: ils utilisent la même formule. Et elle est loin de donner une solution exhaustive au problème, car, comme une formule physique, elle se base sur un tas d'hypothèses ici très simplificatrices et sous-estime donc dans certains cas la corrélation. Le modèle n'est d'abord pas prévu pour décrire ce qu'il se passe dans un environnement extrême, mais seulement lorsqu'il se situe autour d'un «état moyen». Ici, l'espace des possibilités n'est pas binaire, comme pour le cas des assurances vie (mort ou vivant). En particulier, le marché est supposé liquide, ce qui n'est pas du tout le cas dans les cas de crise. Le modèle est inefficace lorsque quelque chose affecte un grand nombre de personnes en même temps (la baisse des prix des logements par exemple). De plus, l'approche de Li ne fait aucune allocation à l'imprévisibilité. Elle suppose que la corrélation est une constante, alors que selon Paul Wilmott, chercheur en finance quantitative, «les corrélations entre les quantités financières sont notoirement instables» et qu'il est impensable d'établir une théorie sur des paramètres imprévisibles. Enfin, l'attente pour la compilation d'une base de données historiques (se basant sur des défauts de paiement réels, qui sont rares) nécessaires au fonctionnement du modèle et donc à la détermination de la corrélation était trop longue. C'est pourquoi David Li a considérablement simplifié le problème en utilisant soit une base de données limitée, qui ne peut selon lui «couvrir toutes les possibilités», soit directement les prix des CDS pour évaluer la corrélation. Autrement dit, dans le second cas, si le prix d'un Swap tend à faire bouger celui d'un autre dans la même direction, on en déduit que leur corrélation est importante. Cela suppose que les marchés financiers en général, et plus particulièrement celui des CDS, sont capables de donner le prix d'un titre de manière exacte. La formule est en fait comprise à l'envers. On déduit les risques de corrélation de défaut de paiement à partir des prix établis par les agences de notations. Elle ne prend même pas la peine d'essayer de tracer tous les rapports presque infinis entre les divers prêts constituant un paquet, elle s'est contenté du nombre final de corrélation, propre, simple, et qui résume tout. Mais d'autres, comme Nassim Nicholas Taleb, auteur du Cygne noir, vont plus loin en remettant totalement en cause la formule pensant que l'association des risques n'est pas mesurable en utilisant la corrélation car l'histoire passée n'est pas prédictive du futur. D'autres facteurs entrent en jeu comme la situation macro-économique d'un pays par exemple. Selon lui, «Tout ce qui relève de la corrélation est de l'escroquerie».
II. A la recherche du coupable
Doit-on alors réellement pointer du doigt David Li? Ou plus généralement, doit-on remettre en cause les quants et leur finance quantitative? Certains leur reprochent d'être hors de la réalité, appliquant leur expertise académique au monde de la finance et manipulant des chiffres qui ne représentent plus rien, faisant passer l'intelligence numérique devant l'instinct et l'expérience des traders classiques. Cependant, selon Harry Pajer, professeur de statistique et mentor de Li à Waterloo, «Tous les modèles sont faux, mais certains sont utiles». La formule de Li a en effet a clairement été une percée positive dans le monde de la finance pendant cinq années, un morceau de technologie financière qui a permis à des risques très complexes d'être modélisés avec toujours plus de facilité et d'exactitude qu'avant. De plus, Li a juste écrit un article. Un nouveau parallèle avec la physique s'impose alors selon Pajer: lui imputer la responsabilité de la crise serait comme imputer celle d'Hiroshima à Albert Einstein. Li n'a pas mis le feu à Wall Street, il a juste fourni l'allumette. Certains lui reprochent cependant de s'être voilé la face sur l'extrême complexité du problème et d'avoir présenté sa formule comme «résumant tout». En 2005, Li a pourtant déclaré dans The Wall Street Journal, que «La chose la plus dangereuse est quand les gens croient tout ce qui sort du modèle», en précisant que le sien ne s'appliquait pas dans tous les environnements. Cependant, les banquiers gagnaient à cet instant trop d'argent pour prendre en compte ces mises en garde. Aveuglement volontaire ou non, la formule a été utilisée à outrance à des fins non prévues par le modèle. Ils auraient du noter que les résultats beaucoup moins volatils que prévus impliquaient que le risque s'était déplacé ailleurs. Mais où? Ils n'ont pas su, ils n'ont pas demandé. Selon Steeve Brown, professeur à l'Université de mathématiques de Waterloo, «Les modèles sont seulement aussi bons que leurs hypothèses. Si l'on ignore ses hypothèses, il peut produire des choses qu'il n'avait jamais prévu de produire». Le modèle donnait l'impression d'éliminer définitivement le risque, ce qui n'est jamais possible en finance. Il était trop difficile à comprendre pour ses utilisateurs mais malheureusement trop facile à appliquer. David Li avait déjà avertit en 2005 que «Très peu de personnes comprennent l'essence même du problème». On peut alors parler de la responsabilité des banques, et plus particulièrement de leurs mathématiciens, qui faute d'avoir un résultat exact, se contentent et privilégient sa simplicité et sa rapidité.
La formule elle-même a alors un réel pouvoir d'attraction, une élégance. Celle de Li est en effet très simple, en voici une succincte explication:
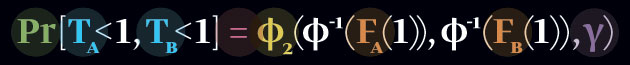
Elle représente la probabilité commune des défauts de paiement de deux titres A et B. C'est ce que les investisseurs recherchent. Elle fait intervenir:
-Les temps de survie de A et B : le temps entre le moment présent et celui auquel le titre subit un défaut de paiement.
-La copule : couple les probabilités des défauts A et B. Son application donne un unique chiffre final.
-Les fonctions de distributions : donnent les probabilités des temps de survie de A et de B. Incertaines, leur moindre erreur peut entraîner une sous-évaluation notoire des risques.
-Gamma : paramètre de la corrélation, c'est lui qui la réduit à un nombre constant. C'est aussi lui qui a rendu la formule irrésistible.
Cette formule est censée résoudre l'immense problème de la corrélation en une seule ligne, c'est pourquoi elle a suscité un tel engouement, comparable à celui provoqué par celle de Black and Scholes au début des années 1980'. Cette dernière a dicté Wall Street pendant deux décennies, mais ne traite en aucun cas le problème de la corrélation. La formule de David Li, aussi inexacte soit-elle, s'inscrit donc en réponse à l'une des limites de Black and Scholes. Comme on l'a vu, elle simplifie cependant elle-aussi drastiquement la réalité, afin de pouvoir espérer la modéliser.
La réflexion est la même pour les autres modèles mathématiques, et donc pour la finance quantitative en général. L'intervention de l'humain est très délicate, autant en tant qu'objet à modéliser aux comportements imprévisibles et imbriqués, qu'en tant qu'utilisateur de la formule, ne tenant pas forcément compte de toutes ses limitations. La justesse d'un modèle mathématiques s'apprécie alors par son adéquation au réel, cependant c'est parfois paradoxalement le réel qui se plie aux règles du modèle.
Sources :
Controverse Mathématiques & Finance. Haut de page.
GILLET, LETOURNEAU, MAGNIEN, MARCILHACY, VYARAVANH-GIRARD