Le calibrage des modèles
Le calibrage consiste à déterminer à partir des données de marché les paramètres du modèle qui permettent le mieux de retrouver les prix du marché. [QUI]
Dans notre modèle simpliste précédent la seule donnée sur laquelle nous pouvons jouer est la moyenne ![]() . C’est assez simple à mettre en oeuvre. Pour des modèles plus compliqués, il peut exister plusieurs dizaines de variables à calibrer correctement, parfois corrélées entre elles.
. C’est assez simple à mettre en oeuvre. Pour des modèles plus compliqués, il peut exister plusieurs dizaines de variables à calibrer correctement, parfois corrélées entre elles.
Cette calibration est un des points faibles des modèles utilisés car il les fait perdre en robustesse étant donné qu’elle est dépendante de la personne qui l’utilise.
« Le prix de n’importe quel instrument est donné par son espérance mais celle-ci dépend de comment on la modélise, de sa volatilité, de sa moyenne : c’est subjectif. »
Analyste quantitatif
De plus, un autre élément inhérent au marché financier complique la tâche de calibration. « Les lois de la finance ne sont pas des lois physiques, et l’on ne peut pas répéter une expérience » [NEK]. Ainsi, à l’inverse de la physique, on ne peut fixer le système et ne jouer que sur une seule variable. Toute la complexité du système s’exprime à chaque instant et de façon entremêlée.
Parfois, les modèles existent mais la calibration est tellement chaotique qu’ils en deviennent inutilisables. C’est notamment le cas de la modélisation des taux d’intérêts,trop sensibles aux événements externes, notamment politiques.
Et si les événements sont rares, on se rend bien compte que calibrer ces paramètres, leur donner des valeurs qui feront sens, est mission impossible.
Michel Fliess
Dans cette remarque de Michel Fliess, on comprend que plus les modèles sont compliqués, c’est à dire qu’ils ont beaucoup de paramètres, plus la calibration sera compliquée. On voit donc ici une tension entre d’un côté, une théorie complète qui prendrait énormément de paramètres en compte mais qui serait complètement inutilisable à cause de la calibration; et de l’autre côté, une théorie plus approximative, simplifiée avec un nombre de paramètres bien plus réduit mais dont la calibration est beaucoup plus simple.
L’approche probabiliste est-elle vraiment pertinente ?
Si l’on s’intéresse à la formule de Black-Scholes, une des choses qui est frappante à première vue est l’indépendance vis à vis du passé. En effet, la formule de valorisation ne dépend que du temps de maturation et de la date actuelle. Autrement dit, cette approche Black-Scholes suppose que demain ne dépend que d’hier.
En l’absence de toute nouvelle information, le cours d’aujourd’hui est la prévision la plus robuste du cours de demain. [MAR]
Selon Frédéric Marty, chargé de recherche en économie au CNRS, cette approche favorise le développement de bulle spéculative quand aucune information supplémentaire n’est disponible. Dans la crise des subprimes, les cours des logements étaient jugés pérennes impliquant une augmentation du nombre de nouveaux crédits et à terme la formation d’une énorme bulle immobilière.
To exhibit well defined probability laws in quantitative finance, in economics and management, and in other social and psychological sciences, where the environmental world is much more involved than in any physical system. [FLI]
Pour Michel Fliess, les probabilités ne sont vraiment pas adaptées dans des domaines tels que la finance quantitative qui s’apparente à l’étude de comportements humains. Il propose une approche dénuées de probabilités : les séries temporelles.
Le but est ici de dégager une tendance dans les cours pour prévoir l’évolution des prix. En effet, sous certaines hypothèses assez lâches, le cours boursier peut se décomposer de la façon suivante :
![]()
C’est cette fonction ![]() qui est la tendance. La fonction
qui est la tendance. La fonction ![]() est supposée à fluctuations rapides, c’est à dire qu’elle varie rapidement autour de zéro et sur chaque intervalle assez grand, son intégrale est nulle.
est supposée à fluctuations rapides, c’est à dire qu’elle varie rapidement autour de zéro et sur chaque intervalle assez grand, son intégrale est nulle.
L’avantage de cette approche est de se séparer de toutes hypothèses économiques ou de comportements qui comme nous l’avons vu précédemment sont parfois contestables. Sur la figure suivante, on voit que la tendance diminue significativement le retard d’estimation par rapport à la moyenne classique.
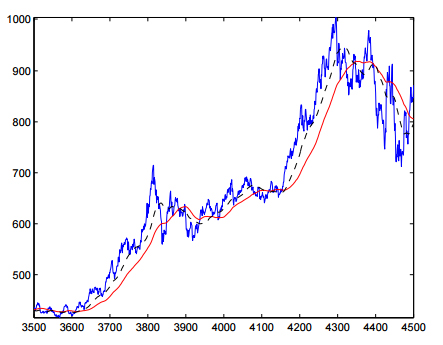
En bleu, cours de l’or. En pointillé, la tendance calculée. En rouge, moyenne glissante classique.
Si l’Homme échoue ainsi dans la modélisation du risque, c’est peut être qu’il est incapable de prendre des décisions dans un univers autant incertain que celui des marchés financiers.