Le mouvement brownien…
Le mouvement brownien a été décrit pour la première fois par le botaniste Robert Brown en 1827 en observant le mouvement de particules à l’intérieur de grains de pollen. C’est donc un phénomène découvert par l’expérience et qui a une réalité physique. Une des descriptions élémentaires utilisées en physique est la suivante : la particule se déplace en ligne droite jusqu’à ce qu’elle rencontre une autre particule ou une paroi qui modifie sa direction et l’accélère.

De façon plus rigoureuse, on peut dire que le mouvement de la particule est aléatoire et son déplacement statistiquement nul. C’est-à-dire qu’elle se déplace autour de son point de départ. Ce processus aléatoire et discontinu rend la modélisation mathématique difficile pour l’époque. C’est Louis Bachelier qui, en 1900, propose dans sa thèse Théorie de la Spéculation la première description mathématique du mouvement brownien.
Sa définition est la suivante : c’est un processus stochastique ![]() gaussien, à accroissements indépendants, stationnaires. Il reste à définir les termes employés.
gaussien, à accroissements indépendants, stationnaires. Il reste à définir les termes employés.
Un processus stochastique ![]() est une suite indexée par le temps de variables aléatoires
est une suite indexée par le temps de variables aléatoires ![]() . A chaque instant
. A chaque instant ![]() , c’est la variable aléatoire
, c’est la variable aléatoire ![]() qui va se réaliser.
qui va se réaliser.
Un processus à accroissements indépendants signifie que l’accroissement ![]() pour
pour ![]() est indépendant des processus précédents
est indépendant des processus précédents ![]() .
.
Enfin, un processus à accroissements gaussiens stationnaires signifie que l’accroissement est une variable aléatoire normale centrée en ![]() et de variance
et de variance ![]() , c’est-à-dire vérifiant la loi de gauss.
, c’est-à-dire vérifiant la loi de gauss.
L’étude du mouvement brownien est toujours d’actualité car il a de nombreuses applications en thermodynamique, en diffusion et bien évidemment en finance.
…appliqué aux marchés financiers
Pour modéliser la dynamique des cours de la bourse, on peut utiliser le mouvement brownien. Si on note ![]() le rendement d’un actif au temps
le rendement d’un actif au temps ![]() on a alors :
on a alors :
C’est la superposition d’une dérive ![]() et d’un bruit gaussien
et d’un bruit gaussien ![]() . L’amplitude de ce bruit est donnée par
. L’amplitude de ce bruit est donnée par ![]() .
.
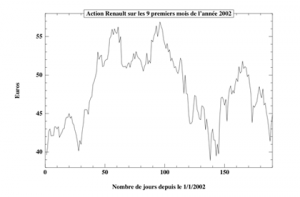
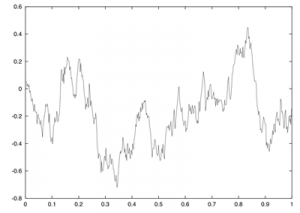
Cette modélisation a quelques impacts sur les hypothèses nécessaires que doivent vérifier les marchés. Le fait que les accroissements soient indépendants implique que l’on ne peut battre le marché, c’est-à-dire qu’on ne peut prévoir les mouvements du marché en utilisant les données passées. Le fait que les accroissements soient gaussiens stationnaire implique que l’on accepte une modélisation gaussienne de la volatilité qui est en réalité la modélisation du risque de l’actif. Si la première hypothèse est économiquement viable, c’est la deuxième qui est au cœur de la controverse car elle donne très peu d’importance aux événements rares qui sont pourtant la cause des grands krachs boursiers.