Pour respecter le cadre d’utilisation d’un modèle en physique comme en finance, les utilisateurs doivent être familiers des hypothèses sur lesquelles le modèle repose.
On peut repérer des hypothèses qui ne sont pas respectées par les modèles mathématiques. [IDI]
Selon le mathématicien Benoît Mandelbrot, l’ingénierie financière se trompe potentiellement puisqu’elle utilise en majorité les travaux de Bachelier (1900) qui reposent sur trois hypothèses, que nous avons tenté de confronter à leurs critiques :
- la loi des grands nombres : si la taille de l’échantillon / le nombre d’observations est assez grand, on respecte la loi statistique et les fluctuations aléatoires deviennent aléatoires.
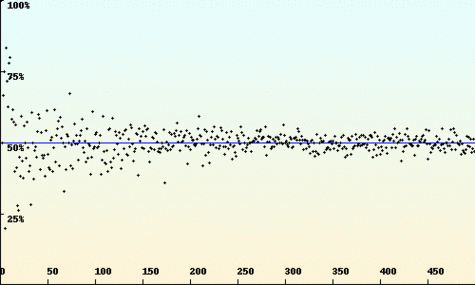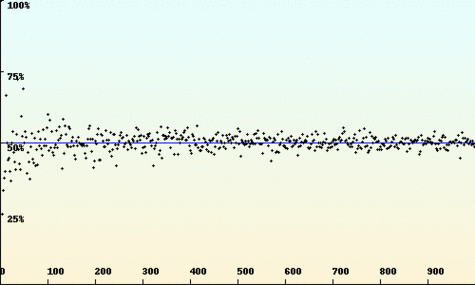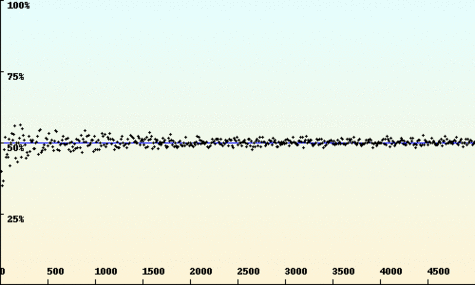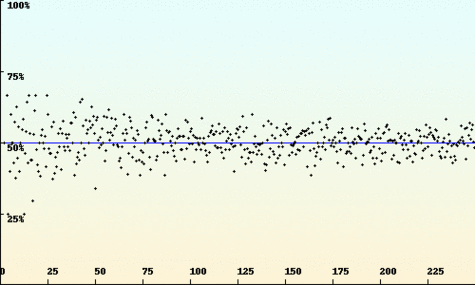
- le théorème central dit gaussien : avec un grand nombre d’observations, une variable aléatoire (comme le prix d’un actif) peut être modélisé par une gaussienne.
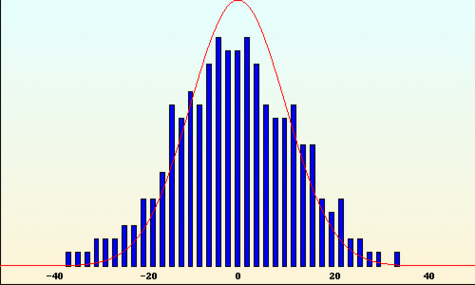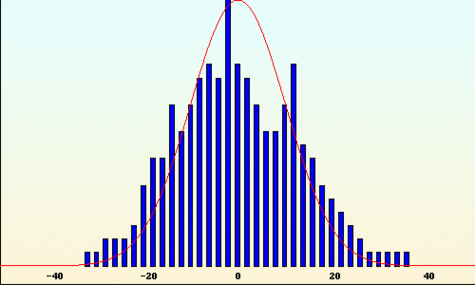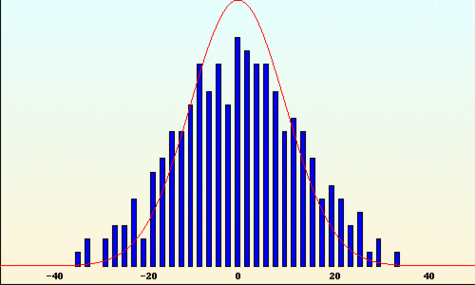
- Approche de Benoît Mandelbrot
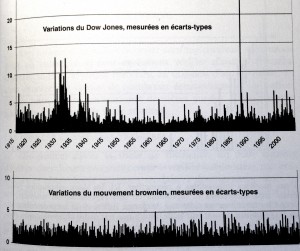
Comparaison des variations du Dow Jones et du mouvement brownien, mesurées en écart type [MAN]
Sur l'image ci-dessous, on peut comparer deux courbes, la première correspondant aux variations réelles du Dow Jones, la seconde correspondant à une modélisation brownienne. La majorité des variations de l'original sont faibles, ce qui est convenablement modélisé sur la deuxième courbe. En revanche, les pics qui apparaissent entre 1930 et 1935 puis en 1987 sur la première courbe ne figurent pas sur la deuxième : ils correspondent à des évènements très rares voire impossibles à en croire la modélisation. En ces points, les deux courbes ne coïncident pas.
Pour Mandelbrot, les variations des cours dépendent fortement des variations précédentes. Les périodes de turbulences ont de grandes chances d'êtres suivies de turbulences plus extrêmes encore ; les pics sont regroupés. Les cours ont tendance à suivre leur propre progression. On peut ainsi repérer des tendances en observant les sauts au cours du temps. Les trois courbes suivantes représentent respectivement les cas "anti-persistant" (orienté dans une direction, le phénomène opposé se produit et la courbe repart en sens inverse), le cas brownien classique qui représente le modèle financier standard (chaque variation ne dépend pas des précédentes) et le cas "persistant" (les tendances significatives apparaissent et les cours suivent leur progression). Dans ce dernier, la courbe prend des valeurs positives ou négatives sur de plus grands intervalles temporels que sur les deux autres graphes. On y retrouve une approche géométrique : la structure de la courbe reste identique en "zoomant" sur une partie du graphe. Le motif est conservé à toutes les échelles.
Mandelbrot introduit alors une nouvelle échelle temporelle, le temps boursier, qui se différencie du temps d'horloge, pour mieux modéliser les fluctuations.
Les aléas boursiers sont caractérisés par la discontinuité et la concentration du risque dans le temps, ce qu’il modélise par ce qu’il appelle un "hasard sauvage". Les fluctuations ne suivent pas de courbe gaussienne.
L'axiome qui stipule que le présent est indépendant d'un passé suffisamment éloigné. Autrement dit, il n'y a pas de tendance, ce que réfutent Michel Fliess et Benoît Mandelbrot, chacun avec leur théories qui se présentent comme une alternative aux modèles dits standard.
Selon Mandelbrot, la théorie de la finance s'organise autour de trois axes [IDI] :
- le Capital asset pricing model (CAPM), qui trouve son origine dans les travaux de Bachelier, et son développement dans les années soixante grâce à William Sharpe (expliqué dans Historique -> modèle B&S)
- la théorie moderne du portefeuille (MPT), développée par Harry Markowitz dans les années soixante
- la formule d’évaluation des options de Black et Scholes développée dans les années soixante-dix (expliquée dans Historique ->modèle B&S)
Voici les trois hypothèses principales du système économique actuel:
- Il n’y a pas d’opportunités d’arbitrage : un acteur ne peut pas gagner de façon sûre sans prendre de risques. En effet, dans ce cas, tout le monde exploiterait cette opportunité, et la tendance serait immédiatement corrigée par le marché. Cette hypothèse se traduit mathématiquement dans le modèle par l’utilisation du calcul stochastique, qui permet de modéliser la nature aléatoire des marchés. Le calcul stochastique est une branche de la théorie des probabilités et permet d’étudier les phénomènes aléatoires qui dépendent du temps.
- Un utilisateur doit fixer de nombreux paramètres avant de pouvoir utiliser un modèle. En régime normal, ces paramètres ne varient que très peu, ce qui garantit la stabilité du modèle. Néanmoins, dès qu’un acteur fait rapidement et fortement varier ces paramètres, il pousse le modèle à la limite de ses possibilités et s’expose au risque de sortir du régime normal, au delà duquel son fonctionnement n’est plus satisfaisant.
Dans l’équation de Black-Scholes, c’est par exemple le cas de la volatilité σ qui est supposée être une constante.
- Tous les modèles supposent que l’économie n’est pas dans un régime extrême, qui est notamment caractérisé par des acteurs au comportement irrationnel. Les modèles sont conçus pour fonctionner en régime normal et pas en régime de crise, ce qui explique pourquoi le système ne fonctionne plus convenablement lorsqu’un événement rare ou imprévisible survient, comme par exemple pendant les krachs boursiers.
Il dénonce également la fausseté de deux autres hypothèses sur lesquelles repose la théorie financière, concernant les acteurs : - La rationalité des acteurs, qui cherchent à s’enrichir. - Le fait que tous les investisseurs se ressemblent.
La question du respect des hypothèses de base soulève un autre problème : comment utiliser les modèles et gérer les événements rares ? Si, après la crise de 2007-2008, on a beaucoup reproché à la finance son excès de mathématiques, nombreux sont les spécialistes qui s’expriment en faveur du renforcement de la prédiction d’événements rares et extrêmes par les mathématiques. Cette nouvelle question mène à des tensions sur le rôle des acteurs : qui sont ces acteurs dont les actions ont entraîné la crise ? Ont-ils eu trop confiance en leur produits financiers et formules mathématiques ?
Nous tenterons de répondre à ces questions dans la suite de l’exposé. Mais tout d’abord, si certaines hypothèses fondatrices des modèles sont fausses, la réalité qu’ils décrivent est-elle vraiment la bonne ?